Patterns within VECMA are abstractions that describe, in a non-application specific manner, a workflow or algorithm for conducting validation, verification, uncertainty quantification or sensitivity analysis. Two classes of pattern are developed within the project: Uncertainty Quantification Patterns (UQPs), focussed on uncertainty quantification and propagation or sensitivity analysis, and Validation & Verification Patterns (VVPs), concerned with validation and verification. The remainder of this document is a lightly edited excerpt from the proposal describing the planned UQPs and VVPS (note that in proposal what we now call patterns were referred to as primitives).

In the VECMA proposal we presented an initial list of UQPs which we intended to cover the different cases that we anticipated in our exemplar application portfolio. This is not intended as an exhaustive list and during the lifetime of the project we have adopted aniterative approach to defining the most useful set of patterns. In the proposal we classified UQPs along two dimensions; control structure and optimization. Below we describe how these properties can be combined to define classes of UQP, an overview of the initially planned UQPs is shown in the figure below.

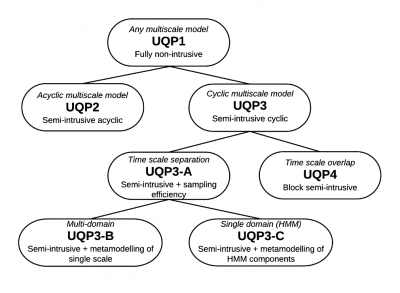Tree chart of the UQPs we aim to design and implement within VECMA, and their mapping to the respective subtypes of multiscale computing applications.

UQP-1: Fully non-intrusive. Performing UQ and SA by using non-intrusive methods on the application as a whole, and quantifying the uncertainty relative to a Quantity of Interest (QoI) that resides in the final application output. By definition this approach cannot identify the contribution to the UQ from individual submodels of a multiscale application. SA will only identify contributions of inputs and parameters that are provided as external input to the overall multiscale application.

UQP-2: Semi-intrusive acyclic In case of acyclic structure, uncertainty propagates in one direction through the multiscale model. Output uncertainty of one single component creates input uncertainty of another component. This UQP performs non-intrusive UQ and SA on consecutive single components. It enables investigation into how uncertainty propagates and becomes amplified within each component of the model.

UQP-3: Semi-intrusive cyclic Perform UQ and SA on each single component within the multiscale model with cyclic structure (varying the inputs of that model to quantify uncertainty relative to a QoI of that model). Because of the cyclic structure, uncertainties no longer propagate in one direction, posing challenges that will be addressed in this project (e.g. by investigating the use of surrogate models). An important class of multiscale models with cyclic structure are multiscale dynamical systems, having a time-integration loop structure.

UQP-4: Block semi-intrusive Single scale models with overlapping time scales are grouped together in blocks. We will adopt advanced, potentially intrusive approaches on these blocks, while retaining a semi-intrusive approach on the remaining single scale components.

UQP-A: Efficient sampling Using techniques (such as qMC, SC, NISP) that are more efficient than basic MC, we can reduce the number of samples required to perform UQ for the given set of input parameters. Or, we subsample the most costly single scale model(s) by some fraction, tolerating an additional error in the estimate of the uncertainties but at the same time drastically reducing the computational demands. This reduces the number of samples required, as well the number of data movements. This UQP can be combined with e.g. UQPs 1-4 above.

UQP-B: Surrogate modelling Replace one or more of the single scale models with simpler and cheaper versions. This reduces the computational cost and communication overhead for each single scale model execution. To replace a chaotic component in a multiscale model (as frequently found in e.g. molecular and climate applications) by a surrogate model, we can for example adopt the stochastic modeling approach.

UQP-C: Surrogate modelling in HMM single domain While executing HMM, we dynamically build surrogates for the microscale models, exploiting the exploration of parameter space, and the HMM database, that is carried out anyway in HMM. This reduces the computational cost and communication overhead for each microscale model execution.

Using this classification, we can then form UQP combinations, for example UQP3-A, Semi-intrusive cyclic with efficient sampling. In this combination of UQP-3 and UQP-A, the efficiency is boosted by exploiting the multiscale structure as well as using efficient sampling methods. The UQ/SA is not entirely independent across single scale models, as the size and type of the UQ/SA sample in at least one component will affect the sampling size and type in other components. In other words, the control structure of the coupled application is modified, but individual single scale models are not. Another example is UQP3-B, Semi-intrusive cyclic with surrogate modelling. In this combination of UQP 3 and UQP B, some of the single-model sampling is performed using simplified models, or surrogate models.

we focus primarily on multiscale V&V, as many single-scale V&V challenges can be addressed using existing tools and libraries. Within the context of multiscale verifications, we will perform five types of verification procedures.

1. Solution verification. Here we investigate the quantities of interest (QoIs) of the application output, when subjected to minor parameter changes to verify self-consistent behavior of the application and detect the presence of numerical artifacts (VVP-1A).

2. Sandbox verification of multiple single scale models. Here we isolate single scale models in the application, and subject them to conventional single scale verification tasks (VVP-1B).

3. Formal verification of the dependency graph of the multiscale application as it is defined in MML (VVP- 2), and semi-automatically the glue code derived from that. This is for example to detect potential deadlocks, or check for consistency in terms of types and scales.

4. Scale range verification for scale bridges. Do the scale bridges deliver outputs that are within the accepted/expected parameter space of receiving single scale model? (range of validity, VVP-3A).

5. Error Propagation. Systematically verify error propagation across different scales through the scale bridging algorithms, while limiting the computational cost of such verification (error propagation, VVP-3A). Multiscale applications require validation against a range of experimental (or benchmark) data sets. It is therefore essential to fully account for the uncertainty found in simulations, and to compare that with the uncertainty of both the source and validation data in question. For the pure purpose of UQ, we can rely on UQPs. However, we will also provide a VVP to enable a systematic comparison of simulation results against a range of validation targets, such as benchmarks or measurements (VVP-1A).

In addition, we provide a specific VVP to enable a so-called validation of added value (VVP-4), performing a dual validation exercise: one of the multiscale application against data, and a second one using only the coarse-grained, single-scale component of the application. The goal of this validation is to quantify the direct added value of using a multiscale approach towards achieving better validation results.